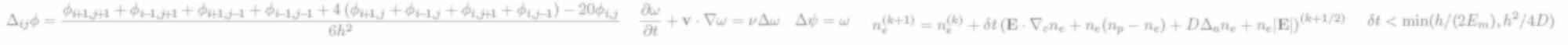
Numerical analysis
Mathematics 5210
Professor: Santiago I. Betelú
| Summary. This course is an introduction to numerical analysis and methods for the solution of partial differential equations. It covers modeling, fundamental discretization theory, error estimation, stability analysis, and approaches for the validation of the numerical codes. This course is practical in nature: the students will learn some theory, but mostly will engage in the solution numerous problems, including heat transport, fluid flow, differential geometry and image processing. Textbooks. Most of the material from the course can be found in the following two books: a) Numerical Methods for Partial Differential Equations, by W. Ames, third edition, Academic Press (1992). b) Numerical solution of partial differential equations, by K.W. Morton and D. F. Mayers, Cambridge Univ. Press (2002). c) Numerical Recipes: The Art of Scientific Computing, by William H. Press, Brian P. Flannery, Saul A. Teukolsky, William T. Vetterling, Cambridge, (1997) (This is the auxiliary text that you will need to complete the homework, you can read some of the chapters of this last book online at www.nr.com). Grading. The grade will be based on two midterms, a final and special projects. Programming We will use Matlab. Little or no previous programming experience needed. The instructor will provide sample programs to "jump start" the learning process. The complexity of the problems we will study resides on the mathematics, not on the programming. |
Example of a project that we will do
in
this course: finite differences
simulation of fluid flow in a box.
(Click in the box with right button to add ink, and move mouse and left
click to add momentum). Other projects involve image
processing, modeling of
shock waves, optimization problems, etc. (see details below).
|
TOPICS WE WILL COVER IN THIS COURSE
Numerical solution of ordinary differential equations:
Finite difference operators.
Forward and backward Euler method and second order methods.
Local and global errors.
Fourth order Runge Kutta method.
Error estimation and control: adaptive timestepping and Runge Kutta of order 4-5.
Implicit integration of nonlinear equations using Newton-Raphson.
Boundary value problems of linear equations: tridiagonal systems and Thomas's algorithm.
Shooting techniques.
Project 1: A nonlinear eigenvalue problem: anomalous diffusion.
Project 2: Computation of the shape of liquids surfaces under the action of capillarity and gravity.
Project 3: Minimal surfaces.
Parabolic equations:
Example: diffusion equations.
Discretization and truncation errors.
Explicit and implicit discretization.
Tridiagonal systems.
Stability analysis.
Convergence.
Crank-Nicolson scheme.
Treatment of boundary conditions: Dirichlet and Neumann boundary conditions. Application to radiation and convection.
Curved boundaries.
Nonlinear equations with free boundaries.
Alternating direction implicit method.
Validation of codes.
Curvature flow.
Project 1: Heat transfer with convection at the boundary.
Project 2: Computation of two-dimensional gas flow in a porous material.
Project 3: Denoising of images using curvature flows.
Elliptic equations:
Boundary value problems as the steady state of an initial value problem.
Jacobi method.
Gauss Seidel method.
Succesive over relaxation.
Rates of convergence.
Alternating direction implicit method for elliptic equations.
Boundary elements method.
Project 1: Steady state heat transfer.
Project 2: Electric potential and capacitance.
Project 3: Fluid flow with vorticity in two dimensions.
Project 4: Interpolation of images.
Hyperbolic flux-conservative initial value problems:
Example: wave equations in one dimension.
Discretization and truncation errors.
Explicit and implicit schemes.
Upstream and downstream discretizations.
Numerical stability and Von Neumann's stability analysis.
Lax method.
Courant-Friedrich condition.
Numerical viscosity.
Staggered leapfrog and Lax Wendroff scheme.
Project 1: Transport
of contaminants by the wind.
Project 2:
Shock waves.
Project 3: Hydraulic jumps.
---------------------------------------------------------------------------------------------------------------------------------
Project 3: Hydraulic jumps.
---------------------------------------------------------------------------------------------------------------------------------