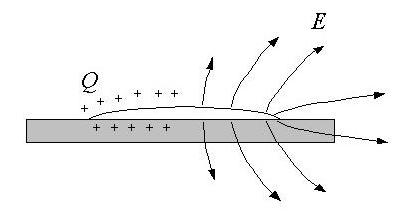
What happens when a charged droplet
spreads on a flat, smooth solid? Here we consider the spreading of a
charged conducting droplet on a flat dielectric surface. Below we
sketch the droplet with a charge Q, which is concentrated at the
surface because the droplet is a conductor. We also show the electric
field lines on the right half. These electric field tries to pull the
droplet apart.
Then two forces drive the spreading: surface tension and electrostatic
repulsion. By using the lubrication approximation we derive a fourth
order nonlinear partial differential equation that describes the
evolution of the height profile. We find that the equation has a
two-parameter family of selfsimilar solutions. Some of the solutions
are explicitly computed while the other solutions are studied
numerically. We show that the solutions have moving contact lines and
the radius of the drop is a power law of time with exponent one-tenth.
We also construct explicit solutions corresponding to non-circular
drops, whose interfaces are ellipses with constant focal length.
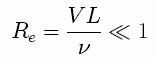

Mathematical formulation:
general equations
As usual, we are going to assume that
the
inertia effects are negligible,
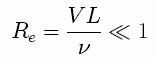
so we can describe the fluid flow
with the Stokes equations, valid both inside and outside the droplet,
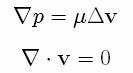
with normal stresses given by (using repeated index summation
convention)
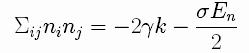
and zero tangential stress
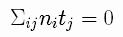
These equations are written using the usual stress tensor for newtonian
fluids
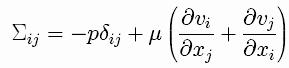
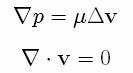
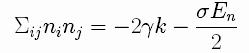
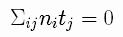
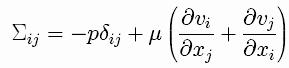
The electric field is assumed to be
electrostatic on the exterior of the drop,
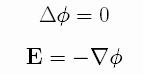
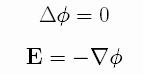
while in the interior, the electric
field is zero, because the drop is made of a conductor fluid. That
means that the electric potential is a constant at the surface. The
surface evolves because the normal component of the surface velocity
equals the normal component of the fluid velocity. At the
solid-liquid interface, the velocity of the fluid is assumed to be zero
(the non-slip boundary condition).
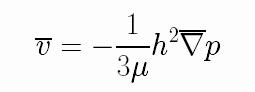
Within this approximation, the pressure is given by
The spreading occurs because the electric field and the charge density
sigma concentrate near the border of the drop. Then a gradient of
pressure is generated between the center of the drop and its border,
which drives the flow.
We approximate the electric field by the field generated by a flat ellipse of negligible thickness with semiaxis a and b. (If the drop is circular, a=b). The corresponding charge density at a position (x,y) at the surface is
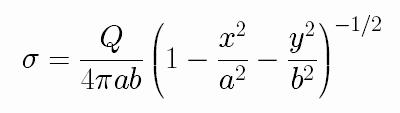
Putting the lubrication equations together with the approximation of the charge density, we obtain a PDE for the drop shape
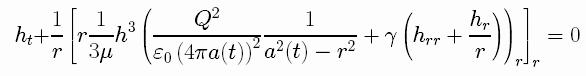

Solution of the fluid flow
equations: lubrication approximation
If the droplet is thin, we can use the lubrication approximation (the
velocity field is supposed to be nearly horizontal, inertia effects
negligible and viscous stressed assumed to be mainly due to the
gradient of the horizontal velocity in the vertical direction). We
assume that the shape of the surface of the drop is a graph of the form
z=h(r,t), then the horizontal velocity field averaged in the
z-direction reduces to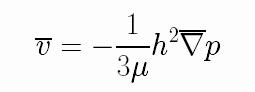
and the profile of velocity is
parabolic in the z-direction
From the conservation of mass, we obtain a PDE for h
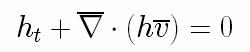
From the conservation of mass, we obtain a PDE for h
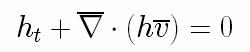

Approximation for the
electric field
We approximate the electric field by the field generated by a flat ellipse of negligible thickness with semiaxis a and b. (If the drop is circular, a=b). The corresponding charge density at a position (x,y) at the surface is
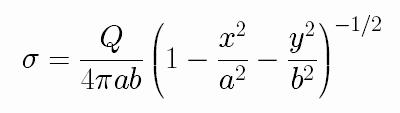
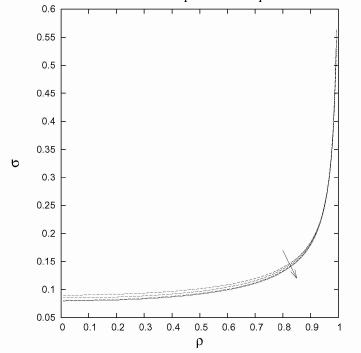
We did a comparison between this
approximation and the ''exact'' charge density as computed with a
3D numerical code. The agreement is excellent provided the drop is
thin (height/radius<0.01). In the figure we show the charge
density versus dimentionless radius rho=r/a for parabolic drops with
a=b. The arrow indicates decreasing values of the ratio height/a= 0.1,
0.05, 0.01

Putting the lubrication equations together with the approximation of the charge density, we obtain a PDE for the drop shape
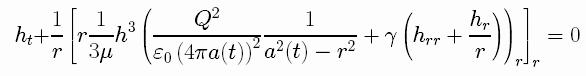
which must be solved subject to the
following initial and boundary conditions:

Selfsimilar solutions
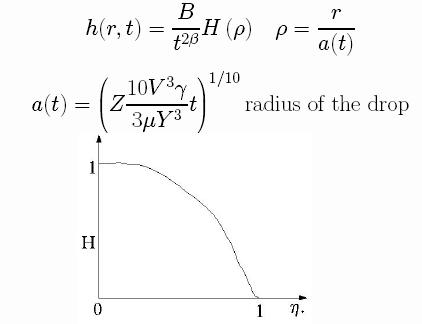
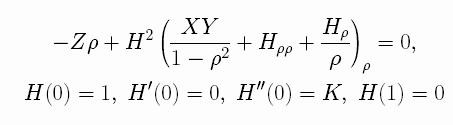
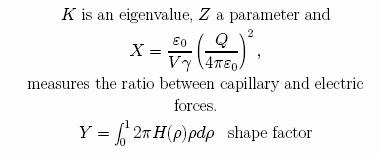
The above PDE
admits solutions of the form

where H(rho)
is the rescaled profile, and is a compactly supported function that
satisfies the ODE and boundary conditions
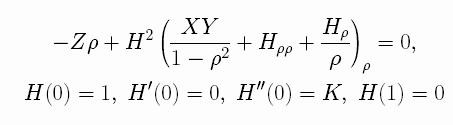
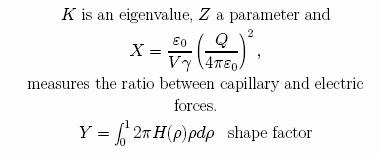
The ODE has
an explicit solution! it is given by
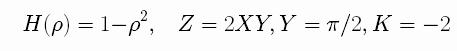
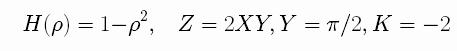
But this is
not the only solution: Others can be found numerically, using a
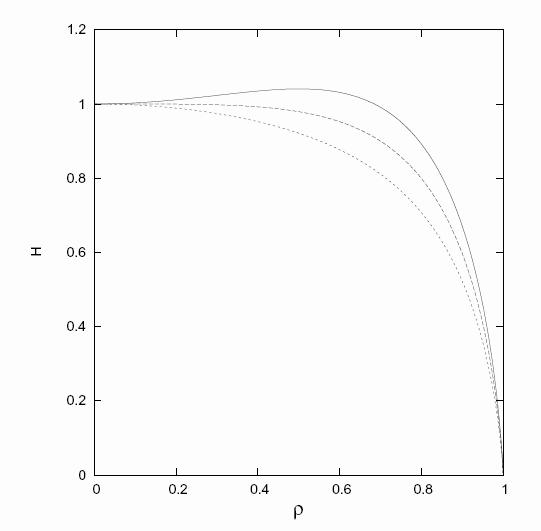
Runge-Kutta scheme for example. Below we depict some profiles:

All the solutions describe a
spreading with a similarity exponent equal to 1/10. The explicit
solution is the least singular of all of them, and it has a finite
slope everywhere. The other solutions have logarithmic singularities
for the derivative at the front, and they have infinite slope
(violating the lubrication approximation), so we suspect that the only
physical solution is the explicit one.
Non-circular solutions
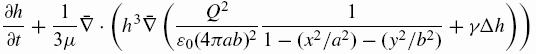
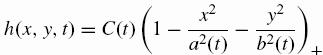
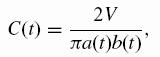
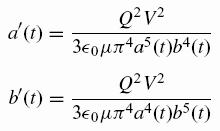
It is
possible to construct solutions where the droplet is an ellipse of
semiaxis a(t) and b(t),
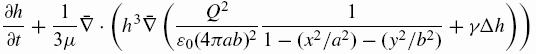
by using an
ansatz of the form
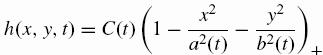
From the
conservation of the volume V, we obtain
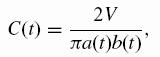
and
by simple substitution into the PDE one finds the equations for the
radii:
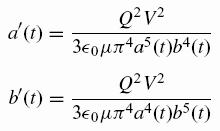
These equations can be solved
explicitly without difficulty, and one finds that the drops have
constant focal length, and that they tend to circles as time approaches
infinity. That appears to indicate that the elliptical drops are stable.