summary

RESEARCH SUMMARY

Fluid flow

My research focuses on the mathematical modelling of fluid flows. The two problems I am currently studying are: a) thin film spreadings on solid surfaces and b) singularities in fluids.
Below is a short list of some recent research problems we tackled with my collaborators:

Spreading of power law fluids: some paints are not newtonian, and their mechanical properties can be approximately described with power law rheology. We developed models for the spreading of these fluids, and found a number of interesting phenomena, such as the non uniqueness of self-similar solutions, and the absence of the paradox of the contact line. Below is a graph of the drop profile given by the many self-similar solutions that describe the spreading of a circular drop.

Spreading of charged fluids: droplets can carry an electrical charge in many natural and man made settings. The electric charge is a powerful driving force of these flows: the electric field, pulls the drop, spreading it over the solid (see figure below). We found that if a conducting fluid spreads on a dielectric, the flow can be described with selfsimilar solutions that have the same exponents than capillary spreading.

Explosion of charged water droplets: they are common in thunderclouds, and their dynamics are not well understood. The charge deforms the drop (see figure below) and finally splits it. We developed numerical methods to study this problem and we are currently exploring the effects of finite conductivity and external electric fields.

Self-similar solutions and singularities on fluid flows. In this setting, singularities represent the divergence of the pressure or the velocity in a given point and time. We recently found numerical evidence indicating that the fluid flow becomes singular at tips generated in finite time in droplets.

Allen cahn dynamics. Recently, I started a new collaboration with Professors Nicholas Alikakos (UNT) and Xinfu Chen (University of Pittsburgh). We are studying the problem of the curvature flow of multiple curves joined by triple junctions. The problem is indirectly related to the fluid flows mentioned above, the connection lies in that under certain boundary conditions, the shape of the free surfaces have the same steady states. In this research, I was able to use my experience in computational differential equations in order to solve the vector Allen Cahn equations. We found the different connections between local minima produce two different kinds of interfaces. This animation shows the formation of interfaces with different connections: on the left we show the interfaces and on the right the three different phases.

One can also solve three dimensional problems. In the image below, we show a surface evolving by curvature flow inside a sphere, obtained with the three dimensional vector Allen Cahn equation.

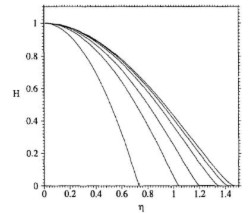
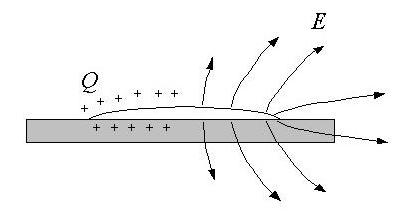
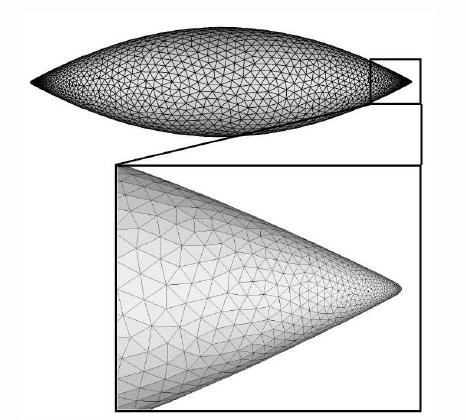
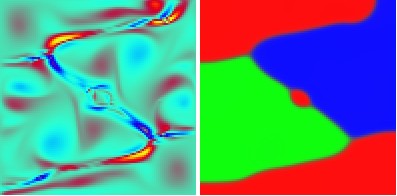
Molecular simulation of cusp formation: the problem is whether a cusp can form at the free surface of a liquid at the molecular scale. Koplik and Banavar found a negative result (Phys. of Fluids 1994 Volume 6, Issue 2, pp. 480-488). However, this was due because they studied the interface between two fluids of similar viscosity. If one repeats the simulation with a fluid-vacuum interface, cusps do appear. The simulation is tricky because the temperature must be carefully controlled. If it is too high, the interface becomes diffuse. In the right range of temperature, we observe cusps as shown in the link below (be patient, the animation has 20MB):

Click to see animation

INTERACTIVE ILLUSTRATIONS

Convergent shallow water flows.

Click link to see animation

Multiphase flow with diffuse interfases: creation of triple junctions

Click on image to see animation (slow)

Convergent flows in the Porous Medium Equation

Simulation of a two dimensional fluid with Navier Stokes equations.

Click link to see animation

OTHER PROJECTS
Done mostly in Minnesota, Kansas and Tandil. I am still engaged in some of these projects.